11. 그래프(2)
- 최소 비용 신장 트리 (MST: Minimum Spanning Tree)
- Kruscal의 MST 알고리즘
- Prim의 MST 알고리즘
- 최단 경로
- Dijkstra의 최단 경로 알고리즘
- Floyd의 최단 경로 알고리즘
- 위상 정렬
11.5 Dijkstra의 최단 경로 알고리즘
Dijkstra's 최단경로 프로그램





Dijkstra's 최단경로 알고리즘 복잡도
: 네트워크에 n개의 정점이 있다면, Dijkstra의 최단경로 알고리즘은 주 반복문을 n번 반복하고, 내부 반복문을 2n번 반복하므로, O(n^2)의 복잡도를 가진다.
11.6 Floyd의 최단 경로 알고리즘
Floyd의 최단경로 알고리즘

: 모든 정점과 정점 사이의 최단경로를 찾는다.
Floyd의 최단경로 알고리즘 아이디어
- A^k[i][j]: 0~k까지의 정점만을 이용한, 정점 i~j로 가는 최단경로 길이
- A^-1(초기상태: 가중치 행렬) --> A^0 --> A^1 --> ... --> A^n-1 순으로 최단경로를 구해간다.
▷ 0~k까지의 정점만을 이용하여, 정점 i~j로 가는 최단경로

: 중간에 정점 k를 거칠 때와 거치지 않을 때의 weight의 sum을 비교하여, 최단경로를 새롭게 업데이트할지 말지를 결정한다.
Floyd의 최단경로 알고리즘 - Example


Floyd의 최단경로 프로그램

Floyd의 최단경로 알고리즘 복잡도
: 네트워크에 n개의 정점이 있다면, Floyd의 최단경로 알고리즘은 3중 반복문을 실행하므로, 시간 복잡도는 O(n^3)이 된다.
11.7 위상 정렬 (topological sort)
- 방향 그래프(DAG: Directed Acyclic Graph)에서 edge <u, v>가 있다면, 정점 u는 정점 v를 선행한다.
--> 방향 그래프 정점들의 선행 순서를 위배하지 않으면서, 모든 정점들을 나열한다.
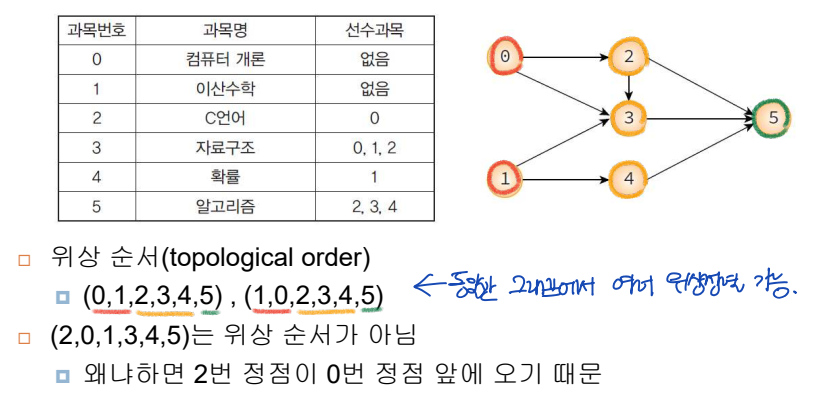
위상 정렬 알고리즘

위상 정렬 - Example

위상 정렬 프로그램





출처: 이화여자대학교 이숙영교수님 자료구조
'자료구조' 카테고리의 다른 글
| [자료구조] 1124 (1) | 2023.12.02 |
|---|---|
| [자료구조] 1121 (2) - 12. 정렬 (0) | 2023.11.28 |
| [자료구조] 1110 (0) | 2023.11.11 |
| [자료구조] 1107 (1) | 2023.11.10 |
| [자료구조] 1103 - 10. 그래프 (1) (0) | 2023.11.04 |



