[자료구조] 13. 탐색

1. 탐색이란?
   • 탐색키: 항목과 항목을 구별해주는 키
2. 정렬되지 않은 배열에서의 탐색
   • 순차탐색(sequential search)
     : 정렬되지 않은 sequence에서 처음부터 마지막까지 순차적으로 하나씩 검사하는 방법 --> O(n)
3. 정렬된 배열에서의 탐색
   • 이진탐색(binary search)
     : 정렬된 배열의 중앙에 있는 값을 조사하여, 찾고자 하는 항목이 그 값보다 작은지 큰지 판단하여, 탐색의 범위를 반으로 줄여가며 탐색한다. --> O(log(n))
   • 색인 순차탐색(indexed sequential search)
     : 인덱스 테이블을 먼저 검사하여, 탐색키가 속한 범위를 알아낸 후, 순차탐색한다.
   • 보간탐색(interpolation search)
     : 배열[0]과 배열[n-1] 값을 통해 탐색키가 존재할 위치를 예측하여 탐색한다.
     - 이진탐색과 유사하나, 리스트를 불균등하게 분할한다. (균등하게 분포되어 있을 것이라고 예측하는 것)
4. 이진 탐색 트리 
   • 이진탐색 vs. 이진탐색 트리
     • 이진탐색(binary search): 자료들이 순차적으로 저장되어 있다. --> 삽입/삭제가 비효율적
     • 이진탐색 트리(BST): 삽입/삭제가 빠르다.
   • 균형 이진탐색 트리 vs. 불균형 이진탐색 트리
     • 균형 이진탐색 트리: O(log(n))
     • 불균형 이진탐색 트리: O(n); 순차탐색과 똑같다. --> 균형트리로 만들자! AVL 트리!
       
5. AVL 트리
   : 모든 노드의 왼쪽과 오른쪽 서브트리의 높이차가 1인 이진탐색 트리--> 새로운 노드가 삽입되어 트리가 불균형 상태가 되면, 스스로 노드들을 재배치하여 균형상태를 유지한다.
6. 2-3 트리

 

---

13.1 탐색이란?

• 항목: 탐색의 단위
• 탐색키(search key): 항목과 항목을 구별시켜주는 키(key)

--> 탐색: 여러 항목 중에서 원하는 탐색키를 가지고 있는 항목을 찾는 것

 

---

13.2 정렬되지 않은 배열에서의 탐색

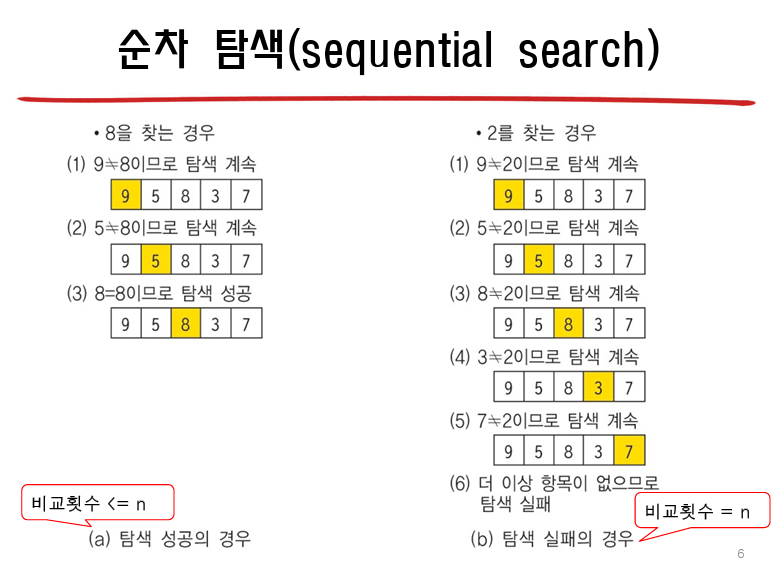
순차 탐색(sequential search)

: 정렬되지 않은 배열의 항목들을 처음부터 마지막까지 하나씩 검사하여 원하는 항목을 찾아가는 방법

순차 탐색(sequential search)

순차 탐색(sequential search)

 

개선된 순차 탐색

: 리스트의 마지막에 탐색키 값을 저장한다.

순차탐색 vs. 개선된 순차탐색

개선된 순차탐색

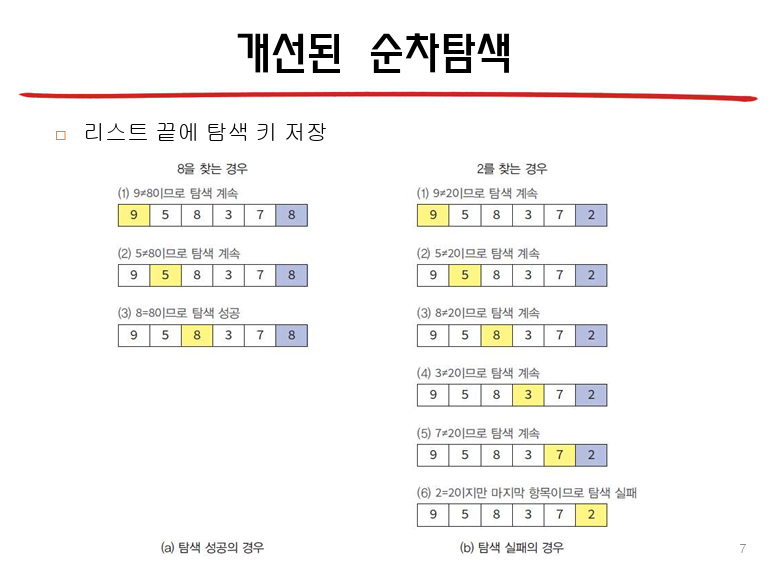
--> 만약 리스트에 키값 2가 없다 하더라도, 리스트의 마지막에 미리 탐색키 값 2를 저장시켰으므로, 반복문을 탈출하게 된다.

 

순차 탐색의 시간 복잡도

순차 탐색의 시간 복잡도

 

---

13.3 정렬된 배열에서의 탐색

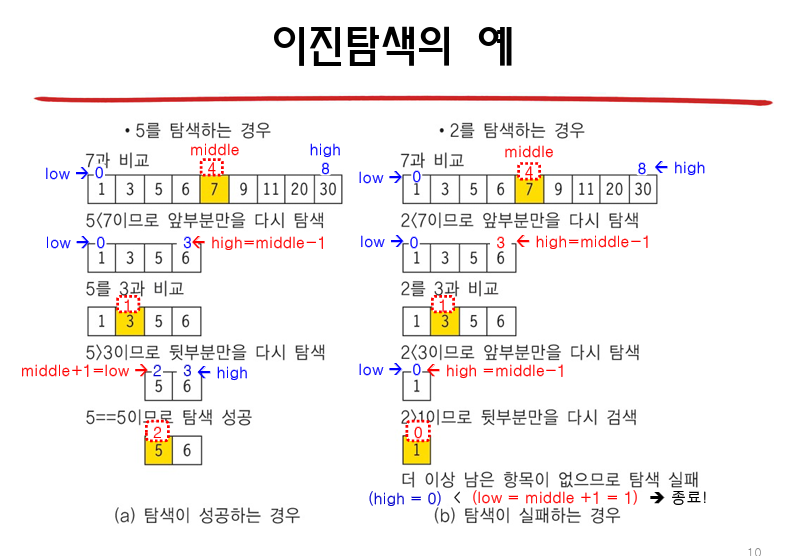
이진 탐색(binary search)

: 배열의 중앙에 있는 값을 조사하여, 찾고자 하는 항목이 왼쪽 또는 오른쪽 부분 배열에 있는지를 알아내어, 탐색의 범위를 반으로 줄인다.

• 이진 탐색에서는 비교가 이루어질 때마다 탐색의 범위가 반으로 줄어든다. --> log(n)

이진탐색 - 예

 

이진탐색 알고리즘

 

이진탐색 구현 - 순환 호출 버전

이진탐색 구현 - 순환 호출 버전

 

이진탐색 구현 - 반복적인 버전

이진탐색 구현 - 반복적인 버전

 

 

색인 순차 탐색(indexed sequential search)

: 인덱스(index) 테이블을 사용하여 탐색의 효율을 높이는 방법

색인 순차 탐색(indexed sequential search)

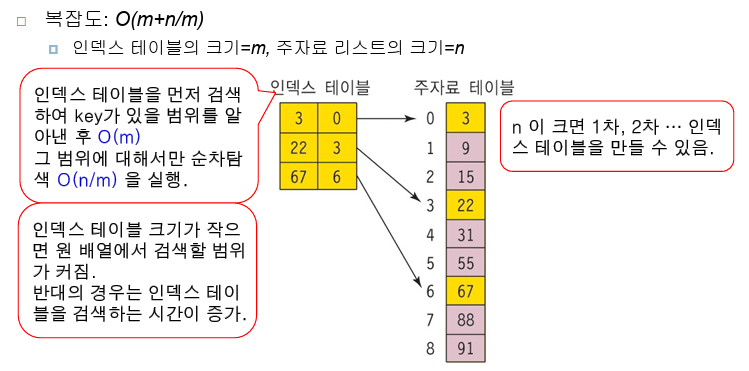
1. 인덱스 테이블에서 index[i] <= key < index[i+1]을 만족하는 항목을 찾는다.
2. 인덱스 테이블에서 위의 조건을 만족하는 항목부터 주 자료 리스트에서 순차 탐색을 수행한다.

 

보간 탐색(interpolation search)

: 탐색키가 존재할 위치를 예측하여 탐색하는 방법

• 보간 탐색은 이진 탐색과 유사하나, 리스트를 반으로 분할하지 않고 불균등하게 분할하여 탐색한다.

보간 탐색(interpolation search)

보간탐색 - 예

 

---

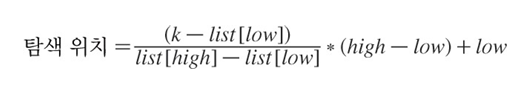
13.4 이진 탐색 트리(binary search tree)

• 이진 탐색(binary search): 자료가 정렬되어 있으므로, 삽입/삭제가 비효율적이다.
• 이진 탐색 트리(binary search tree): 빠르게 삽입/삭제할 수 있다.

균형 이진 탐색 트리

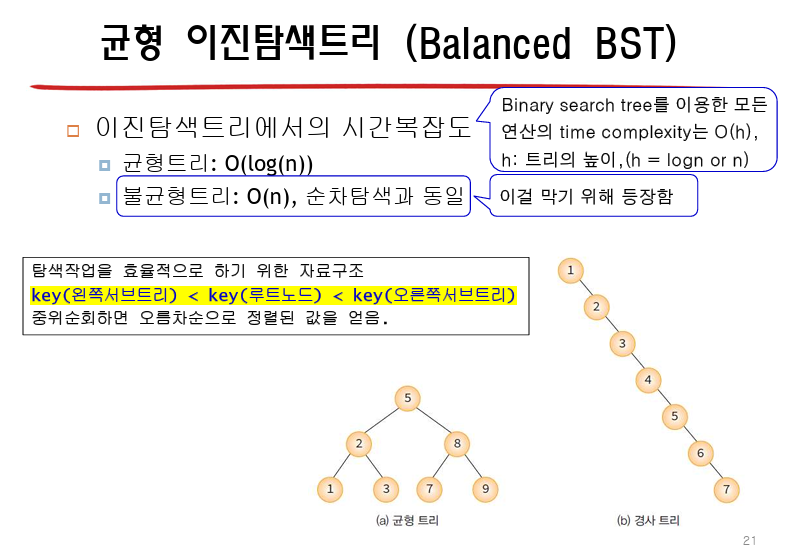
--> 이진 탐색 트리에서는 균형을 유지하는 것이 중요하다!

 

---

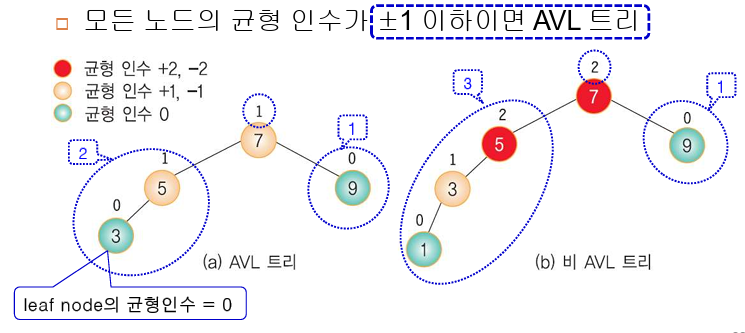
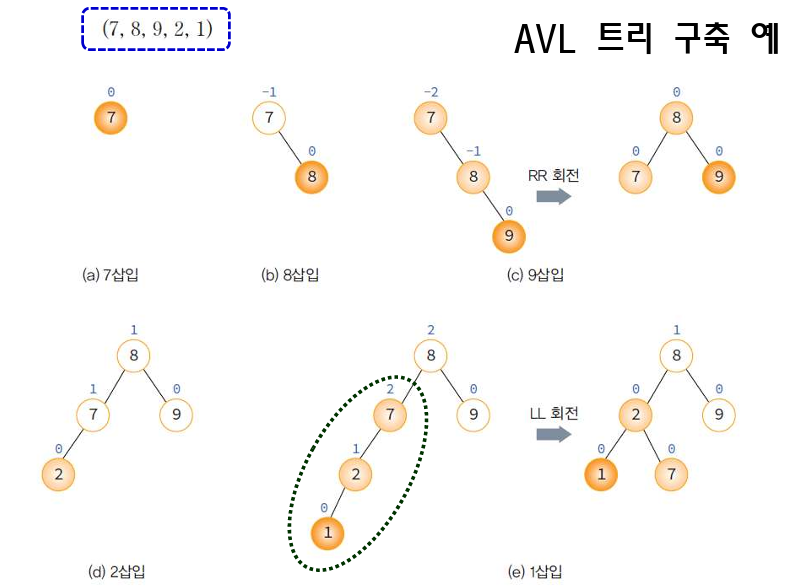
13.5 AVL 트리

: 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 차이가 1 이하인 이진 탐색 트리

• 균형 인수(balance factor) = 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이

--> 트리가 비균형 상태로 되면, 스스로 노드들을 재배치하여 균형 상태로 만든다.

AVL 트리

AVL 트리 삽입 전/후

 

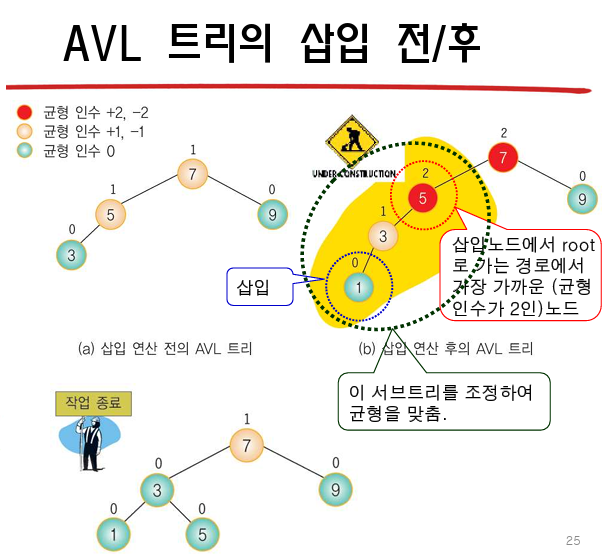
4가지의 경우

LL 회전: 오른쪽 회전

RR 회전: 왼쪽 회전

RL 회전: 오른쪽 회전 --> 왼쪽 회전

LR 회전: 왼쪽 회전 --> 오른쪽 회전

 

AVL 트리 구축 - 예

 

---

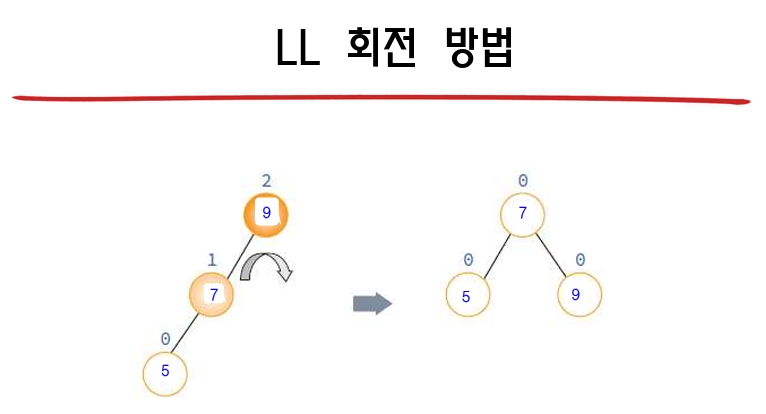
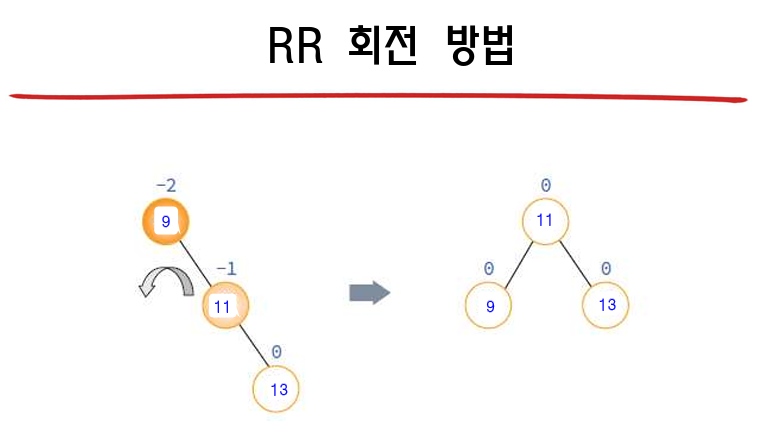
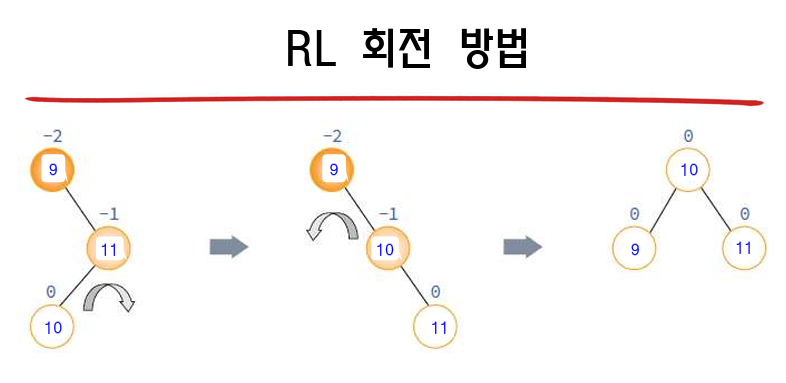
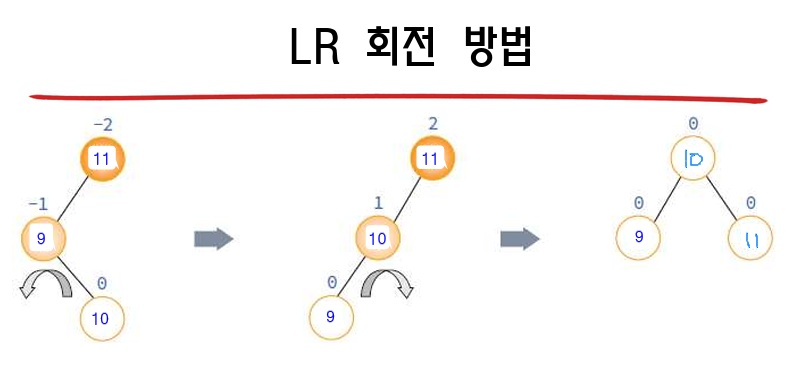
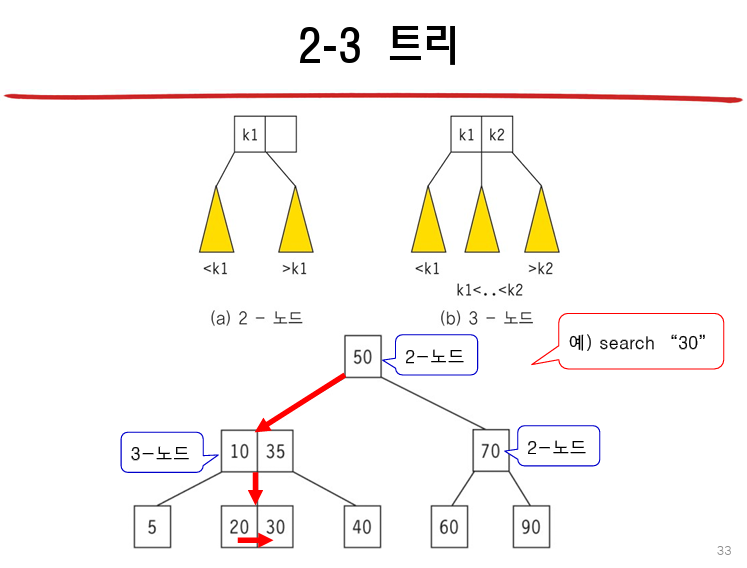
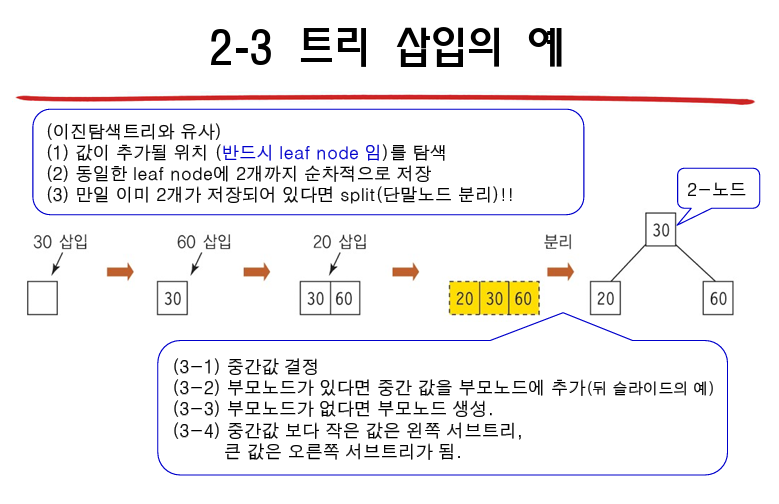
13.6 2-3 트리

: 차수가 2 또는 3인 노드를 가지는 트리

--> 하나의 노드가 두 개 또는 세 개의 자식 노드를 가진다.

2-3 트리

2-3 트리 삽입 - 예

 

 

 

 

 

출처: 이화여자대학교 이숙영교수님 자료구조