- 최소 비용 신장 트리 (MST: Minimum Spanning Tree)
- Kruscal의 MST 알고리즘
- Prim의 MST 알고리즘
- 최단 경로
- Dijkstra의 최단 경로 알고리즘
- Floyd의 최단 경로 알고리즘
- 위상 정렬
11.1 최소 비용 신장 트리 (MST: Minimum Spanning Tree)
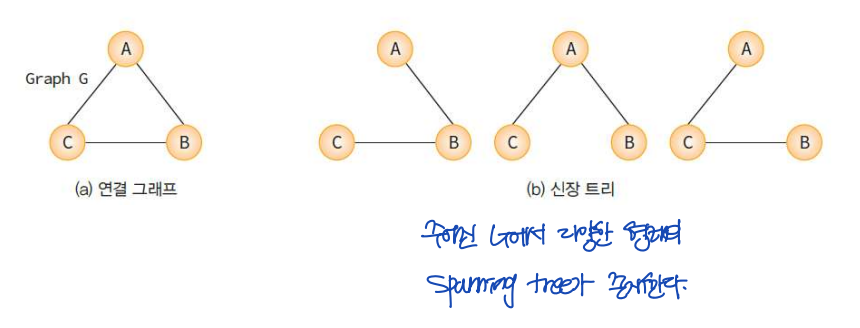
▶ 신장 트리 (spanning tree)
: 그래프 내의 모든 정점을 포함하는 트리
- 트리: 사이클x

▶ 깊이 우선 탐색 (DFS) 신장 트리 알고리즘
- DFS 알고리즘: 모든 정점들을 탐색하여, 만약 그 정점을 방문하지 않았다면, 방문되었다고 표시한다.
- Spanning tree 알고리즘: 만약 그 정점을 방문하지 않았다면, (v, u)를 신장 트리 간선이라고 표시한다.
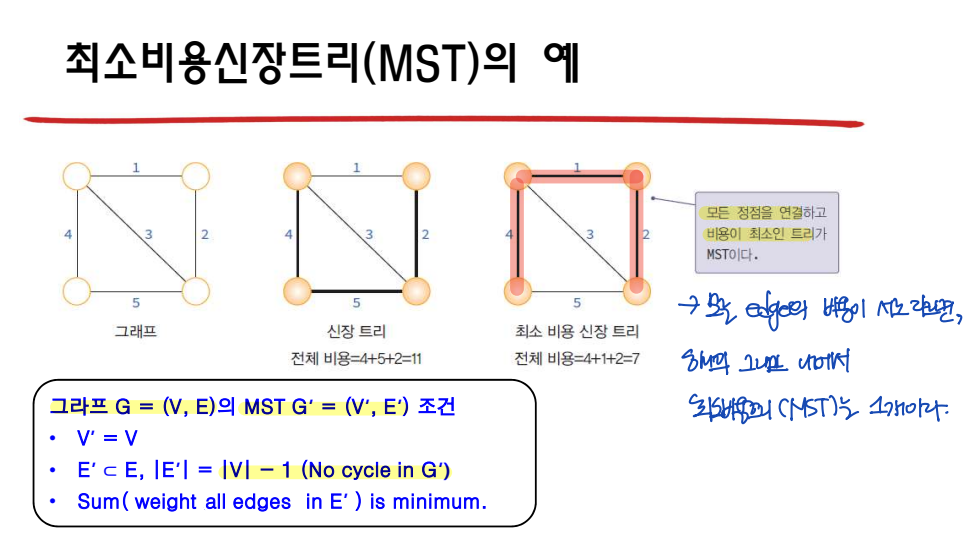
최소 비용 신장 트리 (MST: Minimum Spanning Tree)
: 모든 정점들을 가장 적은 수의 간선, 비용으로 연결하는 트리
- Weighted graph; 비용
11.2 Kruscal의 MST 알고리즘
: 모든 edge들을 검사하여 least-weighted edge를 찾고, 그 edge가 사이클을 만들지 않으면 추가한다.
- union-find 연산: 어떤 edge가 사이클을 만드는지, 만들지 않는지 확인한다.

- encounter: MST에 포함된 edge의 개수 --> MST에 포함된 edge의 개수가 (n-1)보다 작은 동안에,
- k: 검사한 edge의 개수 --> 한 번 시행할 때마다 검사한 edge의 개수를 늘리고, (검사는 weight가 작은 순서대로 함)
- 만약 그 edge가 사이클을 생성하지 않으면, MST에 해당 edge를 추가하고,
- encounter: MST에 포함된 edge의 개수 --> MST에 포함된 edge의 개수를 1개 늘린다.

▶ "사이클을 만들지 않는" --> 사이클을 만드는지 검사해야 한다.

- 새로운 간선이 bridge가 아니라면, 사이클이 형성된다. --> Bridge인 간선만을 추가해야 한다.
- root가 다르다면, 서로 다른 집합에 속해 있는 것이다. --> 두 노드를 연결하는 간선은 bridge이다!
union-find 알고리즘
: 새로운 간선이 bridge인지 판단하기 위해서는, 두 노드가 서로 다른 집합에 속해 있는지 확인해야 한다.
- union(x,y): 원소 x와 y가 속해있는 집합을 입력으로 받아, x와 y를 합쳐서 합집합을 만든다.
- find(x): 원소 x가 속해있는 집합을 반환한다.

--> Kruscal의 알고리즘에서 사용:
- FIND: 어떤 두 노드의 root를 찾아낸다.
--> root가 서로 다르면, 그 두 노드 사이의 edge는 bridge이므로, 그 edge는 사이클을 생성하지 않는다.
--> edge를 추가한다. - UNION: edge가 추가된 두 노드는 이제 하나의 집합에 속하게 되었다.
--> 부모노드를 하나하나 통일하며, 결국 root를 통일한다.


출처: 이화여자대학교 이숙영교수님 자료구조
'자료구조' 카테고리의 다른 글
| [자료구조] 1117 (0) | 2023.11.28 |
|---|---|
| [자료구조] 1114 (0) | 2023.11.26 |
| [자료구조] 1110 (0) | 2023.11.11 |
| [자료구조] 1107 (1) | 2023.11.10 |
| [자료구조] 1103 - 10. 그래프 (1) (0) | 2023.11.04 |



