11. 그래프(2)
- 최소 비용 신장 트리 (MST: Minimum Spanning Tree)
- Kruscal의 MST 알고리즘
- Prim의 MST 알고리즘
- 최단 경로
- Dijkstra의 최단 경로 알고리즘
- Floyd의 최단 경로 알고리즘
- 위상 정렬
11.2 Kruscal의 MST 알고리즘
union-find 알고리즘

: 모든 edge의 weight를 검사해서, 가장 weight가 작은 edge가 사이클을 만들지 않으면, 추가한다.
union-find 프로그램

- set_init: 자기 자신을 root 노드로 초기화한다.
--> parent[i] = -1 - set_find: root 노드를 찾는다.
- set_union: 두 노드가 서로 다른 집합에 속해 있으면(root 노드가 다르면), 합친다.
union-find 연산 - Example

▷ UNION(B, A): B의 root 노드 = A
union-find를 이용한 Kruskal's 프로그램



- qsort: least-weighted edge를 찾는다.
- MST에 포함된 edge의 수 < (node의 수 - 1)인 동안, (<-- MST: tree - 사이클이 없다!)
least-weighted edge를 만드는 두 node가 서로 다른 집합에 속해 있으면(root 노드가 다르면),
두 개의 집합을 합친다.


Kruskal's MST 알고리즘 분석
- qsort: Kruskal 알고리즘은 대부분 간선들을 정렬하는 시간에 좌우된다. --> O(|E|log|E|)
- 사이클 테스트 등의 작업은 정렬에 비해 매우 신속하게 수행된다. --> O(log|V|)
11.3 Prim의 MST 알고리즘
: MST 집합에 인접한 정점 중에서 최저 간선으로 연결된 정점을 선택하여 MST 집합에 추가한다.
- MST 집합에 이미 속한 정점과 인접한 간선들만을 비교하기 때문에, Kruskal 알고리즘과 달리 모든 edge를 비교하지 않는다.
Prim의 MST - Example


Prim의 MST 알고리즘
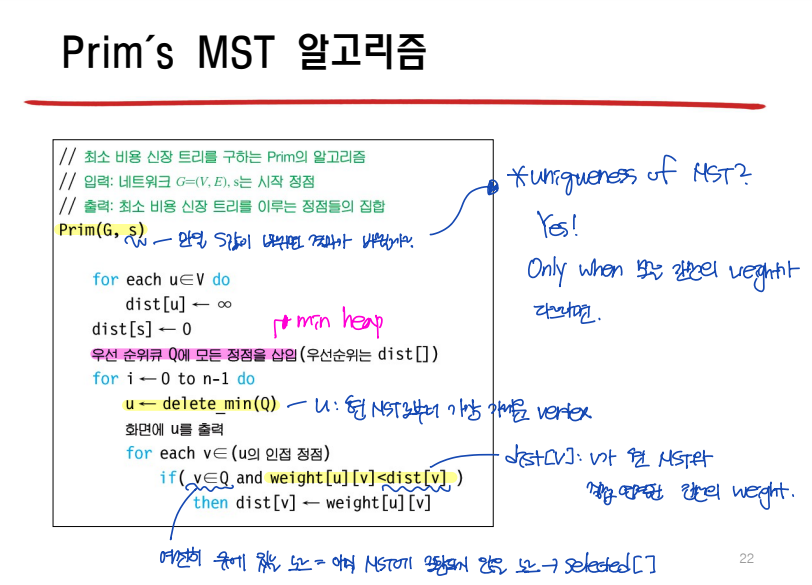
: 현재 MST 집합에 속한 node들과 직접 연결된 edge 중, weight가 가장 낮은 것을 택하여 추가한다.
- 모든 edge의 weight가 다르다면, s(시작 node)가 바뀌어도 Prim의 MST 알고리즘 결과는 동일하다.
Prim의 MST 프로그램






이화여자대학교 이숙영교수님 자료구조
'자료구조' 카테고리의 다른 글
| [자료구조] 1121 (1) (0) | 2023.11.28 |
|---|---|
| [자료구조] 1117 (0) | 2023.11.28 |
| [자료구조] 1110 - 11. 그래프(2) (1) | 2023.11.26 |
| [자료구조] 1110 (0) | 2023.11.11 |
| [자료구조] 1107 (1) | 2023.11.10 |



